python与机器学习入门二

写在开头参考

机器学习算法分类：

• 监督学习（预测）：有特征值和目标值，有标准答案
  • 分类：对应数据类型为离散型
    • k-近邻算法
    • 贝叶斯分类
    • 决策树与随机森林
    • 逻辑回归
    • 神经网络
  • 回归：对应数据类型为连续型
    • 线性回归
    • 岭回归
  • 标注
    • 隐马尔科夫模型
• 无监督学习：只有特征值
  • 聚类
    • k-means

特征选择的方式：

• 过滤式：
  • 低方差特征
• 嵌入式：
  • 正则化
  • 决策树
  • 神经网络

精确率与召回率

先熟悉一个概念：混淆矩阵
在分类任务下，预测结果与正确标记之间存在四种不同的组合，构成混淆矩阵（适用于多分类），构成如下：

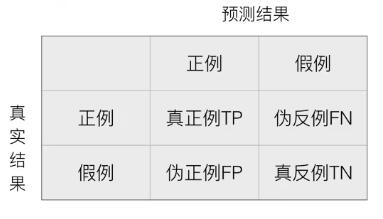
而精确率与召回率都是通过这个矩阵来算的：

其他标准：
F1-score，反映了模型的稳健性，是一个综合评判标准，公式如下：

分类评估模型API：

sklearn.metrics.classification_report(y_true,y_pred,target_name=None)

• y_true:真实目标值
• y_pred:估计器预测的目标值
• target_name:目标类别名称
• return:每个类别精确率与召回率，F1，support(预测的数量)

模型的选择与调优

1.交叉验证：为了让被评估的模型更加准确可信

• 1.将所有训练集数据分成N等分，其中一份作为验证集，其余的当作训练集，然后可以得出一个准确率
• 2.把另一份作为验证集，其余的作为训练集，再得出一个准确率
• 3.一直重复，直到所有数据都作了一次验证集，而此时可以得到N个准确率，将N个准确率求平均值。
  分为几等分则成为 几折交叉验证

2.网格搜索（超参数搜索）：调参数，如k-近邻超参数K的调整
通常情况下，有很多参数是需要手动指定的，如k-近邻算法中的k值，这种叫超参数。但是手动过程繁琐，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

API：sklearn.model_selection.GridSearchCV(estimator,param_grid=None,cv=None)

• estimator:估计器对象，如实例化的KNN估计器knn = KNeighborsClassifier()
• param_grid：估计器的参数(dict),如knn算法中指定的邻近多少个 {“n_neighbors”:{1,3,5}}
• cv:指定几折交叉验证

返回的对象可以执行

• fit:输入训练数据
• score:准确率
• best_score_ : 在交叉验证中的最好结果
• best_estimator : 最好的参数模型
• cv_results_ :每次交叉验证后的测试集准确率结果和训练集准确率结果

过拟合与欠拟合

问题：训练数据训练的很好，误差也很小，为什么在测试集上有问题呢？

机器学习中一个重要的话题便是模型的泛化能力，泛化能力强的模型才是好模型，对于训练好的模型，若在训练集表现差，不必说在测试集表现同样会很差，这可能是欠拟合导致；若模型在训练集表现非常好，却在测试集上差强人意，则这便是过拟合导致的，过拟合与欠拟合也可以用 Bias 与 Variance 的角度来解释，欠拟合会导致高 Bias ，过拟合会导致高 Variance ，所以模型需要在 Bias 与 Variance 之间做出一个权衡。

使用简单的模型去拟合复杂数据时，会导致模型很难拟合数据的真实分布，这时模型便欠拟合了，或者说有很大的 Bias，Bias 即为模型的期望输出与其真实输出之间的差异；有时为了得到比较精确的模型而过度拟合训练数据，或者模型复杂度过高时，可能连训练数据的噪音也拟合了，导致模型在训练集上效果非常好，但泛化性能却很差，这时模型便过拟合了，或者说有很大的 Variance，这时模型在不同训练集上得到的模型波动比较大，Variance 刻画了不同训练集得到的模型的输出与这些模型期望输出的差异。

欠拟合原因及解决办法：

• 原因：学习到的数据特征特少
• 解决办法：增加数据的特征数量

过拟合的原因及解决办法：

• 原因：
  • 原始特征过多，存在一些嘈杂特征
• 解决办法：可通过交叉验证检查是否过拟合
  • 进行特征选择，消除关联性大的特征（很难做）
  • 正则化

L2正则化：
作用：可以使得回归系数w的每个元素都很小，都接近0
优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合

更详细的如何分辨是过拟合还是欠拟合以及如何防止，参考文章：https://zhuanlan.zhihu.com/p/29707029

模型的保存和加载

from sklearn.externals import joblib
scikit-learn中的文件保存格式是 pkl
保存：
joblib.dump(rf,’test.pkl’)

• rf为fit训练好的估计器模型实例

加载：
estimator = joblib.load(‘test.pkl’)

损失函数

损失函数（loss function）是用来估量你模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。

• log对数损失函数：逻辑回归
• ：平方损失函数（最小二乘法）：线性回归
• 指数损失函数：Adaboost
• Hinge损失函数：SVM
• 其它损失函数：0-1损失函数、绝对值损失函数等
  参考：http://www.csuldw.com/2016/03/26/2016-03-26-loss-function/

k-近邻算法（KNN）

####原理与优缺点
KNN是通过测量不同特征值之间的距离进行分类。它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

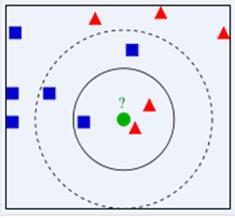
KNN算法的结果很大程度取决于K的选择，如下图，绿色圆要被决定赋予哪个类，是红色三角形还是蓝色四方形？如果K=3，由于红色三角形所占比例为2/3，绿色圆将被赋予红色三角形那个类，如果K=5，由于蓝色四方形比例为3/5，因此绿色圆被赋予蓝色四方形类。

公式：在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离：

k-近邻算法需要做标准化处理

优点：

• 简单，易于理解，无需参数估计，无需训练只需要一次计算就可以得出结果
• 对异常值不敏感
• 适合对稀有事件进行分类
• 可以处理多分类问题

缺点：

• 对测试样本分类时的计算量大，内存开销大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本;
• 可解释性差，无法告诉你哪个变量更重要，无法给出决策树那样的规则;
• K值的选择：k太小，容易受异常点影响，k取值太大，容易受K值数量(类别)波动。可以采用权值的方法（和该样本距离小的邻居权值大）来改进;
• KNN是一种消极学习方法、懒惰算法。

示例

样本数据：

电影名称	打斗镜头	接吻镜头	电影类型
California Man	3	104	爱情片
He’s Not Really into Dudes	2	100	爱情片
Beautiful woman	1	81	爱情片
Kevin Longblade	101	10	动作片
Robo Slayer 3000	99	5	动作片
Amped II	98	22	动作片
？	18	90	未知

如果我们通过公式（如欧氏距离）计算出已知电影与未知电影的距离如下：

电影名称	与未知电影的距离
California Man	20.5
He’s Not Really into Dudes	18.7
Beautiful woman	19.2
Kevin Longblade	115.3
Robo Slayer 3000	117.4
Amped II	118.9

按照距离递增排序，可以找到k个距离最近的电影。假定k=3，则三个最靠近的电影依次是：

• He’s Not Really into Dudes
• Beautiful woman
• California Man
  kNN按照距离最近的三部电影的类型，决定未知电影的类型——爱情片

API与实战demo

API：sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=’auto’)

• n_neighbors:int，可选，默认为5，设置查询默认使用的邻居数
• algorithm：{‘auto’,’ball_tree’,’kd_tree’,’brute’}，可选用计算最近邻居的算法，’ball_tree’将会使用BallTree，’kd_tree’会使用KDTree，auto根据传递给fit的值来自动决定

示例：facebook题目:k近邻算法预测入住位置

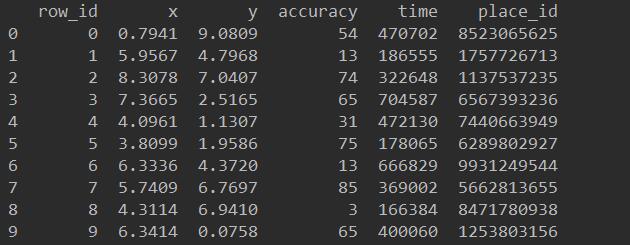
数据集介绍：
本次实验的数据集来自于Kaggle与Facebook合作的机器学习竞赛，旨在通过由facebook提供的2000多万条数据信息预测一个人想要登记入住的地方。
数据来源：https://www.kaggle.com/c/facebook-v-predicting-check-ins/data
其中：
train.csv

• row_id：登记事件的ID
• xy：坐标
• accuracy：定位准确性
• time：时间戳
• place_id：业务的ID，也是预测的目标值

分析思路：

• 数据集预处理
  • 数据量太 → 缩小坐标范围
  • 时间数据 → 转化为年月日（增加新的时间特征，便于后续计算）
  • 类别太多 → 按照指定条件进行转换
• 分割数据及标准化
  • 选定”place_id”为目标值，数据集预处理结果为目标值。
  • 使用StandardScaler类对数据进行标准化处理。
• KNN分类预测
  • 在分类预测过程中，使用超参数搜索API对模型进行选择和调优。

数据的原始内容为：

from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
import pandas as pd


def knncls():
    '''
    k-近邻算法预测用户入住位置
    :return: None
    '''
    # 读取数据
    data = pd.read_csv("./train.csv")
    # print(data.head(10))

    # 特征工程
    # 1.通过设定xy范围缩小数据
    data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")  # query相当于一个查询语句，参数为查询条件

    # 2.处理时间戳数据
    time_value = pd.to_datetime(data['time'], unit='s')  # 将时间戳转换为年-月-日 时-分-秒格式
    # print(time_value)
    '''
    timevalue的值为：
    0          1970-01-06 10:45:02
    1          1970-01-03 03:49:15
    2          1970-01-04 17:37:28
    3          1970-01-09 03:43:07
    '''
    # 把日期转换为字典格式
    time_value = pd.DatetimeIndex(time_value)
    # 3.添加构造一些特征
    data['day'] = time_value.day
    data['hour'] = time_value.hour
    data['weekday'] = time_value.weekday
    # 4.把时间戳特征删除,sklearn中axis为1表示列
    data = data.drop(['time'], axis=1)

    # 5.只保留入住人数大于3的目标位置,生成新的data
    place_count = data.groupby("place_id").count()  # 按照'place_id'进行分组,然后统计次数。groupby使用参考：https://blog.csdn.net/m0_37870649/article/details/80979809
    # print(place_count)
    '''
    此时print的place_count如下：
    此时place_id为索引，而原来的特征值都变为了对应索引的place_id出现了多少次
    place_id    row_id    x    y  accuracy  day  hour  weekday                                        
    1000015801      78   78   78        78   78    78       78
    1000017288      95   95   95        95   95    95       95
    1000025138     563  563  563       563  563   563      563
    1000052096     961  961  961       961  961   961      961
    '''
    place_count_r = place_count[
        place_count.row_id > 3].reset_index()  # 筛选place_count中row_id大于3的，然后通过reset_index()把place_id重新设为特征而不是索引
    train_data = data[data["place_id"].isin(place_count_r["place_id"])]     #通过对比筛选

    # 提取特征值和目标值
    x = train_data.drop(["place_id", "row_id"], axis=1)

    y = train_data["place_id"]

    # 分割数据集
    #参数：特征值，目标值，测试集比例。返回值依次为：训练集特征值、测试集特征值，训练集目标值，测试集目标值
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 对训练集和测试集的特征值进行标准化
    std = StandardScaler()

    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 实例化knn估计器
    knn = KNeighborsClassifier()    # n_neighbors，默认5

    #knn.fit(x_train, y_train)   #参数：训练集特征值、训练集目标值
    # 预测结果
    #y_predict = knn.predict(x_test) #参数：测试集
    # 打印准确率
    #print("准确率为:", knn.score(x_test, y_test))
    '''
    准确率为: 0.4732860520094563
    '''

    # 进阶思考：
    # 交叉验证与网格搜索对K-近邻算法调优
    param = {"n_neighbors": [i * 2 for i in range(1, 5)]}
    gc = GridSearchCV(knn, param_grid=param, cv=5)
    gc.fit(x_train, y_train)

    print("在测试集中的准确率：", gc.score(x_test, y_test))
    print("在交叉验证中验证集的最好结果：", gc.best_score_)
    print("使用的最好的模型：", gc.best_estimator_)
    '''
    在测试集中的准确率： 0.47848699763593383
    在交叉验证中验证集的最好结果： 0.47540983606557374
    使用的最好的模型： KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=None, n_neighbors=8, p=2,
           weights='uniform')
    '''
    return None
if __name__ == "__main__":
    knncls()

朴素贝叶斯算法

使用前提：特征之间独立，不互相影响

该算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题

原理

条件概率中： P(A|B)表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：P(A|B) = P(AB)/P(B)。
通常我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。
贝叶斯公式如下：

其中：

• P(类别)指每个文档类别的概率，计算方式 (某文档类别数 / 总文档数量)
• P(特征|类别) = 指给定类别下特征的概率，计算方式：P(F1|C) = Ni/N
  • Ni为该F1特征词在C类别所有文档中出现的次数
  • N为所属类别C下的文档所有词出现的次数和
• 在比较一个文章属于不同文章类型的概率时，会发现分母P(特征)是相同的，所以可以省略掉

拉普拉斯平滑：
如果词频列表里面有很多出现次数都为0的词，在计算的时候可能使计算结果都变为0，这是不合理的，解决方式就是增加拉普拉斯修正

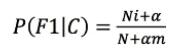
其中，α为指定的系数，一般为1，m为训练文档中统计出的特征词个数。

朴素贝叶斯分类的流程可以由下图表示：

优缺点

优点：

• 算法逻辑简单,易于实现
• 分类过程中时空开销小
• 对缺失数据不太敏感
• 对小规模的数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。

缺点：
理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

示例

一个简单示例如下：

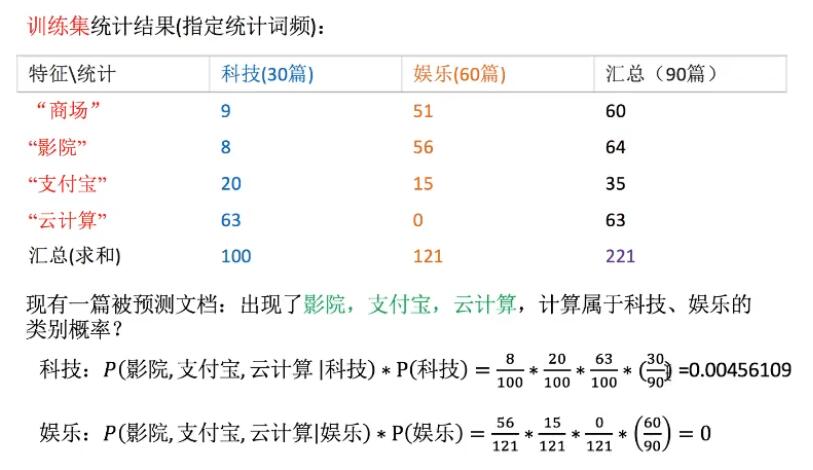
可以看到由于云计算在娱乐文章里出现的频率是0，所以导致最后结果是0，这里需要进行拉普拉斯平滑处理。
即将P(影院，支付宝，云计算|娱乐)计算时的 分子+1，分母+4，

API与实战demo

pythonAPI：sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

• alpha：拉普拉斯平滑系数，默认1

此处的实例用的还是之前内置的sklearn20类新闻分类的数据，20个新闻组数据包含了20个主题的18000个新闻组帖子。

from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB


def naviebayes():
    '''
    朴素贝叶斯对新闻进行分类
    :return: None
    '''
    news = fetch_20newsgroups(subset='all')

    # 进行分割
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)

    # 对数据集进行特征抽取,用tf-idf方法
    tf = TfidfVectorizer()

    # 以训练集中的词的列表进行每篇文章重要性统计
    x_train = tf.fit_transform(x_train)  # 此时x_train为sparse矩阵，大概内容就是记录着:(行，列) 对应数值
    print(tf.get_feature_names())
    '''
    特征名，也就是每个单词
    'davidst', 'davidstern', 'davidw', 'davie', 'daviel', 'davies', 'davinci', 'davis', 'davison',
    '''

    x_test = tf.transform(x_test)

    # 进行朴素贝叶斯算法的预测
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    '''
    大多数是0，因为一篇文章不是所有的词都有，每一行代表一篇文章，列就是上面的特征名，即单词，行列对应值为TF-IDF值
    [[0. 0. 0. ... 0. 0. 0.]
    [0. 0. 0. ... 0. 0. 0.]
    ..................
    [0. 0. 0. ... 0. 0. 0.]]
    '''

    mlt.fit(x_train, y_train)

    y_predict = mlt.predict(x_test)
    print("预测的文章类别为：", y_predict)
    '''
    预测的文章类别为： [ 7 16  0 ...  4  8  1]
    '''

    # 得出准确率
    print("准确率为：", mlt.score(x_test, y_test))
    '''
    准确率为： 0.8293718166383701
    '''
    return None


if __name__ == "__main__":
    naviebayes()

番外篇，R语言与朴素贝叶斯

R语言中的klaR包提供了朴素贝叶斯算法实现的函数NaiveBayes
NaiveBayes(formula, data, …, subset, na.action= na.pass)
NaiveBayes(x, grouping, prior, usekernel= FALSE, fL = 0, …)

• formula指定参与模型计算的变量，以公式形式给出，类似于y=x1+x2+x3；
• data用于指定需要分析的数据对象；
• na.action指定缺失值的处理方法，默认情况下不将缺失值纳入模型计算，也不会发生报错信息，当设为“na.omit”时则会删除含有缺失值的样本；
• x指定需要处理的数据，可以是数据框形式，也可以是矩阵形式；
• grouping为每个观测样本指定所属类别；
• prior可为各个类别指定先验概率，默认情况下用各个类别的样本比例作为先验概率；
• usekernel指定密度估计的方法（在无法判断数据的分布时，采用密度密度估计方法），默认情况下使用正态分布密度估计，设为TRUE时，则使用核密度估计方法；
• fL指定是否进行拉普拉斯修正，默认情况下不对数据进行修正，当数据量较小时，可以设置该参数为1，即进行拉普拉斯修正。

决策树(Decision Tree)和随机森林(Random Forest)

• 决策树是用树的结构来构建分类模型，每个节点代表着一个属性，根据这个属性的划分，进入这个节点的儿子节点，直至叶子节点，每个叶子节点都表征着一定的类别，从而达到分类的目的。
  • 常用的决策树有ID4，C4.5，CART等。在生成树的过程中，需要选择用那个特征进行剖分，一般来说，选取的原则是，分开后能尽可能地提升纯度，可以用信息增益，增益率，以及基尼系数等指标来衡量。如果是一棵树的话，为了避免过拟合，还要进行剪枝（prunning），取消那些可能会导致验证集误差上升的节点。
• 随机森林实际上是一种特殊的bagging方法，它将决策树用作bagging中的模型。首先，用bootstrap方法生成m个训练集，然后，对于每个训练集，构造一颗决策树，在节点找特征进行分裂的时候，并不是对所有特征找到能使得指标（如信息增益）最大的，而是在特征中随机抽取一部分特征，在抽到的特征中间找到最优解，应用于节点，进行分裂。随机森林的方法由于有了bagging，也就是集成的思想在，实际上相当于对于样本和特征都进行了采样（如果把训练数据看成矩阵，就像实际中常见的那样，那么就是一个行和列都进行采样的过程），所以可以避免过拟合。

决策树

信息论基础

在信息论中，熵（英语：entropy）是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。这里，“消息”代表来自分布或数据流中的事件、样本或特征。
熵最好理解为不确定性的量度而不是确定性的量度，因为越随机的信源的熵越大。

香农的信息熵理论：
如果n个事件发生的概率分别为p1,p2,p3….pn则他们的准确信息量应该是：
H = -(p1Logp1 + p2logp2 + p3logp3 + … + pnlogpn)
H的专业术语为信息熵，单位为比特，公式：

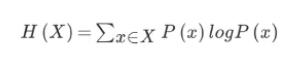
例如，当有32支球队比赛时，猜测谁是冠军，在没有任何信息的情况下，每个球队获胜的概率都是 1/32，此时信息熵为
H = -(1/32Log1/32 + 1/32log1/32 + 1/32log1/32 + … + 1/32log1/32) = 5
而当我们得到一些信息的情况下，比如不同球队的获胜几率为多少，那我们最终得出的信息熵H将会小于5。

信息增益：
当得知一个特征条件之后，减少的信息熵的大小。

决策树的生成

决策树划分依据

1. ID3：信息增益最大
   特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与 特征A给出条件下D的信息条件熵H(D|A) 之差，即公式:
   g(D,A) = H(D) - H(D|A)
   此处信息增益表示，得知特征A的信息而使得类D的信息的不确定性减少的程度，计算H(D)和H(D|A)公式：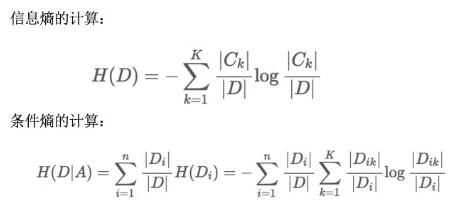

上面这公式有点复杂，举个例子：
有如下银行贷款的数据，通过前面的特征来决定是否可以贷款。

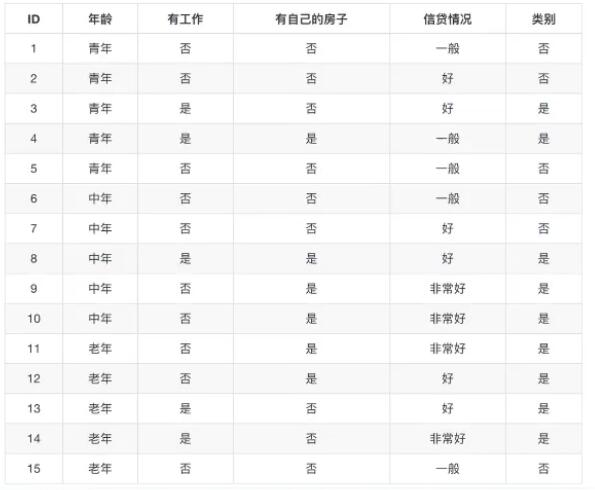
对于没有加入特征之前，只看是否贷款数据的信息熵：一共有15条数据，9条可以贷款，6条不可以。所以此时总的信息熵为：0.971，计算方式如下

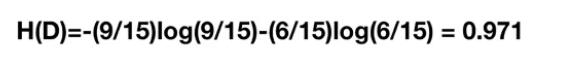
然后我们让A1，A2,A3,A4分别表示年龄，工作，有自己房子和信贷情况四个特征，则分别计算他们的信息增益即可选择下一次决策用什么特征。
此处以年龄为例，而年龄中青年、中年、老年各占5个，即 1/3，根据公式，年龄的信息增益计算为：
g(D,A1) = H(D) - H(D’|年龄) = 0.971 - [1/3H(青年) + 1/3H(中年)+ 1/3H(老年)]，
此时需要计算H(青年)针对类别的信息熵，由于5个青年中，有3个类别是‘否’，2个对应类别是‘是’，所以计算方式如下：
H(青年)= -(2/log2/5 + 3/5log3/5)
中年和老年的计算方式类似，最终结果为：

同理，其他的特征信息增益也可以计算出来，g(D,A2)=0.324,g(D,A3)= 0.420,g(D,A4)= 0.363，相比较A3所对应的有自己的房子这个特征的信息增益最大，所以特征A3为最有特征的一个属性。

2. C4.5：信息增益比最大
3. CART：回归树
   • 回归树：平方误差最小
   • 分类树：基尼系数（Gini）最小，基尼系数的划分更加细致

决策树优缺点

优点：

• 简单的理解和解释，树木可视化
• 不需要太多的数据准备操作，其他技术通常需要数据归一化等操作

缺点：

• 决策树可能过于复杂，而且训练集中正确率高不代表测试集中正确率高，有些异常点会导致结果有误。过拟合

改进：

• 剪枝cart算法
• 随机森林

经典案例：泰坦尼克号乘幸存预测

决策树分类器API：sklearn.tree.DecisionTreeClassifier(criterion=’gini’,max_depth=None,random_state=None)

• criterion:默认是‘gini’系数，也可以选择信息增益的熵’entropy’
• max_depth:树的深度大小
• random_state:随机数种子
  method：
• decision_path:返回决策树的路径

决策树的结构，本地保存API：sklearn.tree.export_graphviz(extimator,outfile=”tree.dot”,feature_names=[‘’,’’])

• extimator：实例化的估计器对象
• outfile：保存路径和文件，必须是后缀dot格式，这格式课方便的转换为pdf，png等格式
• feature_names:特征名，可自己指定

• 用软件graphviz运行命令：dot -Tpng tree.dot -o tree.png 来查看，tree.png改为tree.pdf则转换为pdf

案例数据：http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt
数据中包含的特征：票的类别，存活结果，乘坐版（pclass），年龄，登陆，home.dest，房间，票，船和性别等。其中乘坐班是指乘客班(1,2,3),是社会经济阶层的代表。其中age数据还存在缺失需要处理。
处理流程：

• pd读取数据
• 选择有影响的特征，处理缺失值
• 进行特征工程，pd转换字典，特征抽取x_train.to_dict(orient=”recored”)
• 决策树估计器流程

案例代码如下：

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,export_graphviz

def decision():
    '''
    决策树对泰坦尼克号乘客进行预测生死
    :return:None
    '''
    # 获取数据
    titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

    # 处理数据，找出特征值和目标值,这里以三个为例
    x = titan[['pclass', 'age', 'sex']]
    print(x)
    '''
         pclass      age     sex
    0       1st  29.0000  female
    1       1st   2.0000  female
    2       1st  30.0000    male
    3       1st  25.0000  female
    '''
    y = titan['survived']

    # 缺失值处理
    x['age'].fillna(x['age'].mean(), inplace=True)

    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 进行特征工程，当特征是类别的时候，要进行ont-hot编码
    dict = DictVectorizer(sparse=False)

    x_train = dict.fit_transform(x_train.to_dict(orient="records"))
    print(dict.get_feature_names())
    '''
    ['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male']
    '''
    print(x_train)
    '''
    刚好与上面对应
    [[29.         1.          0.          0.          1.          0.        ]
    [ 2.          1.          0.          0.          1.          0.        ]
    [30.          1.          0.          0.          0.          1.        ]
    '''
    x_test = dict.transform(x_test.to_dict(orient="records"))

    # 用决策树估计器进行预测
    dec = DecisionTreeClassifier()  # max_depth是个超参数，值可以影响结果，也决定了决策树的深度
    dec.fit(x_train,y_train)

    #预测准确率
    print("DecisionTreeClassifier无参数时，预测的准确率为：",dec.score(x_test,y_test))
    '''
    DecisionTreeClassifier无参数时，预测的准确率为： 0.8206686930091185
    '''

    #导出决策树的结构，截图在之后给出
    export_graphviz(dec,out_file="./tree.dot",feature_names=['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=女性', 'sex=男性'])
    return None


if __name__ == "__main__":
    decision()

上述代码保存后的决策树结构图

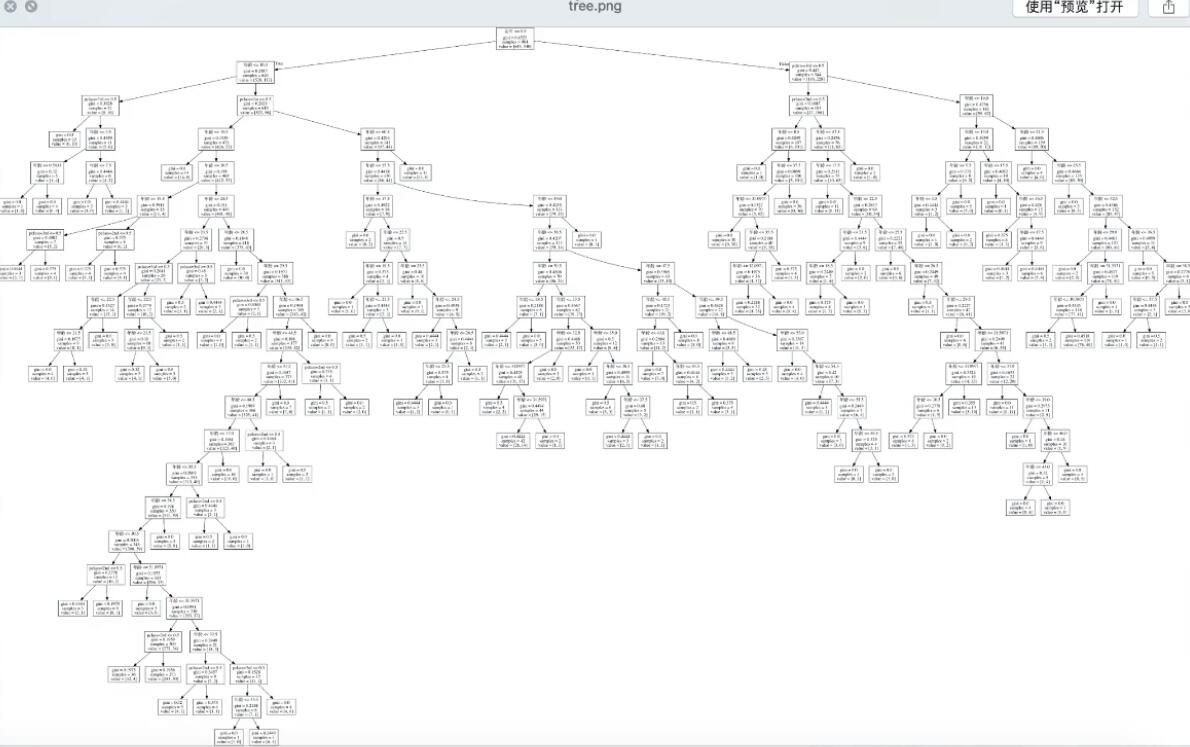
随机森林-集成学习方法

集成学习方法

集成学习（Ensemble learning）通过组合几种模型来提高机器学习的效果。与单一模型相比，该方法可以提供更好的预测结果。
集成学习有一个重要的概念叫Diversity，也就是说每个分类器要长得尽量不一样。就像一个团队，有的人擅长策划，有人擅长拉赞助，有人擅长执行，这样才是一个牛逼的团队。集成学习中每个分类器也要有一定差异，这样才是一个好的集成。

集成学习算法主要有Boosting和Bagging两种类型：

• Boosting：通过迭代地训练一系列的分类器，每个分类器采用的样本的选择方式都和上一轮的学习结果有关。例如在AdaBoost中，之前分类错误的样本有较高的可能性被选到，在之前分类正确的样本有较小的概率被选到。就像你在背单词，你今天总会选择前面几天背不下来的单词，Boosting也会选择前面轮数没学下来的样本。这个类别下面的主要算法是AdaBoost和GBDT。
• Bagging：每个分类器都随机从原样本中做有放回的采样，然后分别在这些采样后的样本上训练分类器，然后再把这些分类器组合起来。简单的多数投票一般就可以。随机森林就是这个类别的一个经典算法，仔细学习你会发现它的每棵树和基本的决策树的不同，非常神奇的算法。

额外拓展：集成方法是将几种机器学习技术组合成一个预测模型的元算法，以达到减小方差（bagging）、偏差（boosting）或改进预测（stacking）的效果。

随机森林的定义，过程，优势

定义：在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

过程：

1. 单个树的建立过程：假如有N个样本，M个特征，随机有放回的抽样，即:Bagging:Bootstrap Aggregating
   • 随机在N个样本中有放回的选择一个样本，重复N次，因为有放回所以可能有重复
   • 随机在M个特征当中选出m个特征
     • m的取值：m<<M
2. 重复1过程，建立多颗决策树，他们的样本和特征大多不一样。

优势：

• 当前所有算法中，具有极好的准确率
• 能够有效地运行在大数据集上
• 能够处理具有高维特征的输入样本，而且不需要降维
• 能够评估各个特征在分类问题上的重要性

随机森林与泰坦尼克号乘客幸存预测

随机森林API:class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0, warm_start=False, class_weight=None)
列举几个重要参数，参数实在太多，超参数也有很多了，需要的时候再搜索好了：

• n_estimators : integer，可选default=10,森林里（决策）树的数目
• criterion : string, 可选(默认值为“gini”)，衡量分裂质量的性能（函数）。 受支持的标准是基尼不纯度的”gini”,和信息增益的”entropy”（熵）
• max_features： int, float, string or None,可选default=”auto”，寻找最佳分割时需要考虑的特征数目，不同的值代表不同的考虑方式：这里n_features为总的特征数
  • 如果是int，就要考虑每一次分割处的max_feature特征
  • 如果是float，那么max_features就是一个百分比，那么（max_feature*n_features）特征整数值是在每个分割处考虑的
  • 如果是auto，那么max_features=sqrt(n_features)，即n_features的平方根值。
  • 如果是log2，那么max_features=log2(n_features)
  • 如果是None,那么max_features=n_features
• max_depth : integer or None, 可选的（默认为None），（决策）树的最大深度。如果值为None，那么会扩展节点，直到所有的叶子是纯净的，或者直到所有叶子包含少于min_sample_split的样本。
• bootstrap : boolean, 可选的(default=True)，建立决策树时，是否使用有放回抽样。

代码示例：处理数据与之前的决策树一样，只是把决策树估计器改成了随机森林，然后进行了网格搜索与交叉验证

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier

def decision():
    '''
    决策树对泰坦尼克号乘客进行预测生死
    :return:None
    '''
    # 获取数据
    titan = pd.read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt")

    # 处理数据，找出特征值和目标值,这里以三个为例
    x = titan[['pclass', 'age', 'sex']]
    print(x)
    '''
         pclass      age     sex
    0       1st  29.0000  female
    1       1st   2.0000  female
    2       1st  30.0000    male
    3       1st  25.0000  female
    '''
    y = titan['survived']

    # 缺失值处理
    x['age'].fillna(x['age'].mean(), inplace=True)

    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

    # 进行特征工程，当特征是类别的时候，要进行ont-hot编码
    dict = DictVectorizer(sparse=False)

    x_train = dict.fit_transform(x_train.to_dict(orient="records"))
    print(dict.get_feature_names())
    '''
    ['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male']
    '''
    print(x_train)
    '''
    刚好与上面对应
    [[29.         1.          0.          0.          1.          0.        ]
    [ 2.          1.          0.          0.          1.          0.        ]
    [30.          1.          0.          0.          0.          1.        ]
    '''
    x_test = dict.transform(x_test.to_dict(orient="records"))

    # 随机森林估计器进行预测，超参数调优(这里以两个参数为例）
    rf = RandomForestClassifier()

    #网格搜索与交叉验证寻找最佳参数
    param = {"n_estimators":[10,20,100,120,200,300,500,800],"max_depth":[5,8,15,20,30]}
    gc = GridSearchCV(rf,param_grid=param,cv=2)
    gc.fit(x_train,y_train)
    print("准确率为：",gc.score(x_test,y_test))
    '''
    准确率为： 0.8267477203647416
    '''
    print("选择的参数模型：",gc.best_params_)
    '''
    选择的参数模型： {'max_depth': 5, 'n_estimators': 10}
    '''
    return None


if __name__ == "__main__":
    decision()

线性回归，迭代的算法

回归问题：目标值是连续的，如房价，营业额等。

定义与原理

线性关系模型：
一个通过属性的线性组合来进行预测的函数:

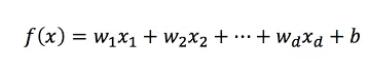
w为权重，b称为偏置项，可理解为w0*1

线性回归定义：

在统计学中，线性回归（Linear regression）是利用称为线性回归方程的最小二乘 函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。

通用公式：
x为特征值，w为要求的值

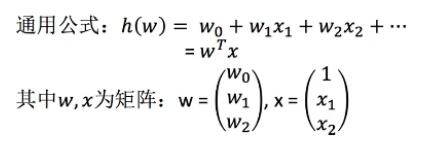
线性回归的损失函数：平方损失函数（最小二乘法, Ordinary Least Squares ）

最小二乘法是线性回归的一种，OLS将问题转化成了一个凸优化问题。在线性回归中，它假设样本和噪声都服从高斯分布（为什么假设成高斯分布呢？其实这里隐藏了一个小知识点，就是中心极限定理），最后通过极大似然估计（MLE）可以推导出最小二乘式子。最小二乘的基本原则是：最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。换言之，OLS是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢（即Mean squared error， MSE），主要有以下几个原因：

• 简单，计算方便
• 欧氏距离是一种很好的相似性度量标准
• 在不同的表示域变换后特征性质不变

下面的式子，f(x)：模型的预测值。Y：真实值
平方损失（Square loss）的标准形式如下：

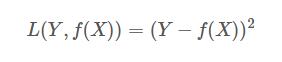
当样本个数为n时，此时的损失函数变为：

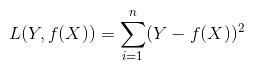
Y-f(X)表示的是残差，整个式子表示的是残差的平方和，而我们的目的就是最小化这个目标函数值（注：该式子未加入正则项），也就是最小化残差的平方和（residual sum of squares，RSS）。

而在实际应用中，通常会使用均方差（MSE）作为一项衡量指标，公式如下:假设有n个数据，后面的减法为 预测值-真实值

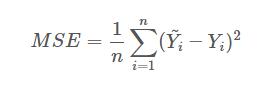
我们通常说的线性有两种情况，一种是因变量y是自变量x的线性函数，一种是因变量y是参数α的线性函数。在机器学习中，通常指的都是后一种情况。

两种求解方法

从前面得知，线性回归要求每个特征对应的权重w值，使得线性回归的损失函数值最小，有两种方法：

1. 最小二乘法之正规方程（不常用）
   X为特征值矩阵，y为目标值矩阵，求解方程如下：

缺点：当特征过于复杂，求解速度太慢

2. 最小二乘法之梯度下降SGD（理解过程） 线性回归中一直在迭代，刚开始是原始值减去后面的学习速率*方向，得到一个新的值，下次迭代用这个新的值继续减去 学习速率*方向。
   使用：面对训练数据规模十分庞大的任务

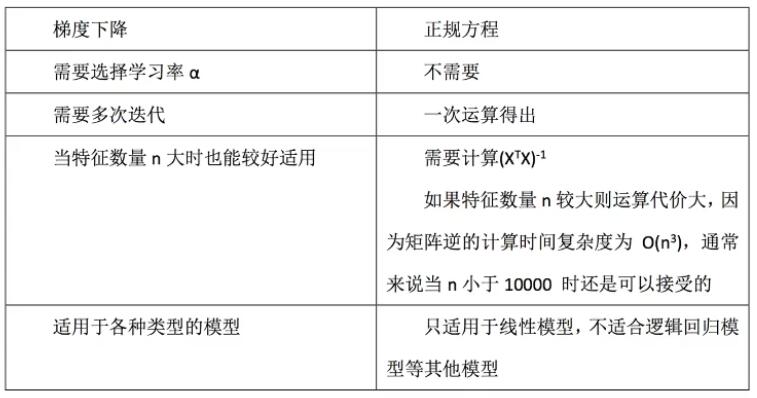
正规方程与梯度下降对比：

API与案例

sklearn.linear_model.LinearRegression()

• 普通最小二乘线性回归
• coef_：求出的回归系数

sklearn.linear_model.SGDRegressor()

• 通过使用SGD最小化线性模型
• coef_:求出的回归系数

均方差算回归损失的API：

sklearn.metrics.mean_squared_error(y_true,y_pred)

• y_true:真实值
• y_pred:预测值
• return：浮点数结果
• 真实值和预测值为标准化之前的值

案例：波士顿房价预测
流程：

1. 数据获取
2. 数据分割
3. 训练与测试数据标准化处理
4. 使用最简单的线性回归模型LinearRegression和SGDRegressor对房价进行预测

代码案例如下：

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error


def mylinear():
    '''
    线性回归预测房子价格
    :return: None
    '''
    # 获取数据
    lb = load_boston()
    # 分割数据集到训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)

    # 进行标准化
    # 这里特征值和目标值都要进行
    std_x = StandardScaler()  # 对特征值进行标准化
    x_train = std_x.fit_transform(x_train)
    x_test = std_x.transform(x_test)

    std_y = StandardScaler()  # 对目标值进行标准化
    y_train = std_y.fit_transform(y_train.reshape(-1, 1))  # 要求是二维
    y_test = std_y.fit_transform(y_test.reshape(-1, 1))

    # estimator预测

    # 正规方程求解方式预测
    lr = LinearRegression()
    lr.fit(x_train, y_train)
    print("回归系数为：", lr.coef_)
    ''''
    回归系数为： [[-0.13482789  0.14684301  0.01549439  0.03522313 -0.21053828  0.32880086
    -0.00599198 -0.39363529  0.25896495 -0.2026098  -0.21658332  0.09938895
    -0.38005182]]
    '''
    # 预测测试集的房子价格
    y_lr_predict = std_y.inverse_transform(lr.predict(x_test))  # 此时的值还是标准化后的,所以要inverse

    print("测试集里每个房子的预测价格：", y_lr_predict)
    '''
    测试集里每个房子的预测价格： [[-5.23859608]
    [39.61950876]
    [35.86414606]
    ......
    [20.31808398]
    [17.36664138]]
    '''
    print("正规方程的均方差：", mean_squared_error(std_y.inverse_transform(y_test), y_lr_predict))
    '''
    正规方程的均方差： 24.203056713653485
    '''
    # 梯度下降进行房价预测
    sgd = SGDRegressor()  # 这里可以指定学习率
    sgd.fit(x_train, y_train)
    print("SGD预测回归系数为：", sgd.coef_)
    ''''
    SGD预测回归系数为： [-0.08189344  0.07032661 -0.03413881  0.10527339 -0.09947185  0.33781714
    -0.04008106 -0.21279579  0.06362954 -0.05064323 -0.19061834  0.10570017
    -0.36071628]
    '''
    # 预测测试集的房子价格
    y_sgd_predict = std_y.inverse_transform(sgd.predict(x_test))  # 此时的值还是标准化后的,所以要inverse

    print("测试集里每个房子的预测价格：", y_sgd_predict)
    '''
    测试集里每个房子的预测价格：[22.25491159 30.38773853 12.72306638 35.68389966 29.69842243 21.70338892
    15.23925266 27.85422604 24.72436984 31.05806439 16.91816538 28.40787834
    ......
    21.3051416  23.92421059 20.83558394 23.80267794 28.17431605 32.1886237
    25.89847536]
    '''

    print("梯度下降的均方差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
    '''
    梯度下降的均方差： 24.303529166136546
    '''
    return None


if __name__ == "__main__":
    mylinear()

岭回归解决过拟合

线性回归LinearRegression 容易出现过拟合，为了把训练集数据表现更好
而岭回归是带有正则化的线性回归

线性回归与岭回归Ridge对比：
岭回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的稳定。在存在病态数据偏多的研究中有较大的实用价值。

具有L2正则化的线性最小二乘法：sklearn.linear_model.Ridge(alpha=1.0)

• alpha：正则化力度
• coef_:求解的回归系数w

上面的案例用岭回归解决：

python

# 岭回归进行房价预测
rd = Ridge(alpha=1.0)  # 这里可以指定学习率
rd.fit(x_train, y_train)
print("岭回归预测回归系数为：", rd.coef_)
''''
岭回归预测回归系数为： [[-0.07357443  0.11581584  0.0248411   0.06555144 -0.17895055  0.27716807
-0.01529063 -0.32589572  0.24111193 -0.19075882 -0.21855738  0.09673899
-0.44673051]]
'''
# 预测测试集的房子价格
y_rd_predict = std_y.inverse_transform(rd.predict(x_test))  # 此时的值还是标准化后的,所以要inverse

print("测试集里每个房子的预测价格：", y_rd_predict)
'''
测试集里每个房子的预测价格： [[33.05501377]
[29.49658894]
......
[19.62373227]
[12.41679022]]
'''
print("岭回归的均方差：", mean_squared_error(std_y.inverse_transform(y_test), y_sgd_predict))
'''
岭回归的均方差： 27.097530207872403
'''

逻辑回归

逻辑回归的输入就是线性回归的式子，而且也是自我学习的过程，要迭代回归
逻辑回归可以做什么，适应场景：二分类问题

• 广告是否会被点击
• 是否为垃圾邮件
• 是否患病
• 金融诈骗

逻辑回归的输入：

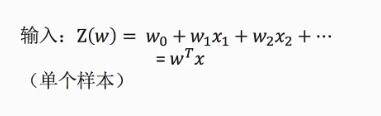
过程：如何从线性回归的输入变为逻辑回归的分类

先了解一下什么事sigmoid函数：将输入转换为0~1，与y轴交叉点默认为0.5

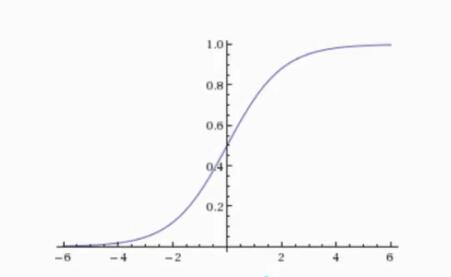
• 横坐标是一个具体的值
• 输出纵坐标是0~1之间的值，可看做概率值

而sigmoid的公式和逻辑回归的公式如下：

• e:常数2.71
• Z：回归的结果

逻辑回归的损失函数：log对数似然损失函数

有些人可能觉得逻辑回归的损失函数就是平方损失，其实并不是。平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到，而逻辑回归得到的并不是平方损失。在逻辑回归的推导中，它假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值等等。而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为：最小化负的似然函数（即max F(y, f(x)) —> min -F(y, f(x)))。从损失函数的视角来看，它就成了log损失函数了。

损失函数公式如下：

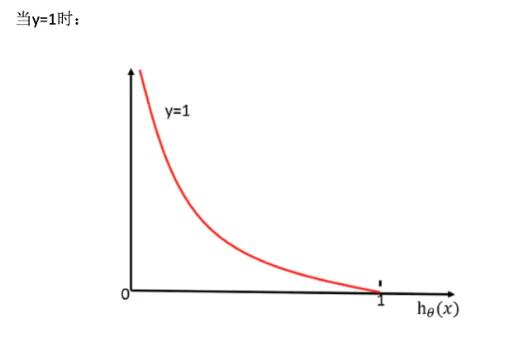
当目标值是1，此时损失值与预测结果为1的概率（x轴）的关系如下：

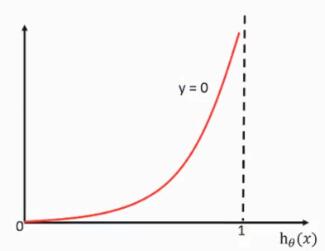
当目标值是0，此时损失值与预测结果为0的概率（x轴）的关系如下：

API与案例：

逻辑回归API：sklearn.linear_model.LogisticRegression(penalty=’l2’,C=1.0)

• penalty:正则化方式
• c:正则化粒度

案例：预测癌症肿瘤（乳腺癌）
数据地址：http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data
数据内容：

• 每个案例11列数据，第一列是检索Id，后9列是与病情相关的医学特征，最后1列表示肿瘤类型的数值
• 肿瘤类型数值：2为良性，占65.5%，4为恶性，占34.5%
  • 注：逻辑回归中，因为针对的是2分类型，所以只有两个结果，只用计算一个概率值来表示属于某一种类型的概率，另一个为(1-概率),而这个概率值一般是数据中占比比较少的那一个类型，比如这里的恶性
• 其中包含几个缺失值，用“？”标出

流程：

• 从网上获取数据
• 数据缺失值处理、标准化
• 估计器流程

代码案例：

from sklearn.metrics import mean_squared_error,classification_report
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
import pandas as pd
import numpy as np

def logistic():
    '''
    逻辑回归做二分类进行癌症肿瘤是否是恶性的预测（根据属性特征）
    :return: None
    '''
    # 构造列标签名字,注：如果数据中没有标签，则pandas会默认把第一行数据作为特征名，这里数据是没有标签名的，所以这里手动添加
    column = ['Sample code number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion','Single Epithelial Cell Size'
              ,'Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
    data = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data"
                , names=column)

    #缺失值进行处理
    data = data.replace(to_replace='?',value=np.nan)
    data = data.dropna()

    # 数据分割
    x_train,x_test,y_train,y_test = train_test_split(data[column[1:10]],data[column[10]],test_size=0.25)

    #进行标准化
    std = StandardScaler()
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    #逻辑回归预测
    lg = LogisticRegression(penalty='l2',C=1.0)
    lg.fit(x_train,y_train)
    y_predict = lg.predict(x_test)
    print("计算的回归系数为：",lg.coef_)
    '''
    计算的回归系数为： [[1.07139763 0.920439   1.03352718 0.88427896 0.07783286 1.15006497
    0.94210002 0.59530658 0.81971895]]
    '''
    print("准确率为：",lg.score(x_test,y_test))
    '''
    准确率为： 0.9590643274853801
    '''
    print("召回率：",classification_report(y_test,y_predict,labels=[2,4],target_names=["良性","恶性"]))
    '''
    召回率：       precision    recall  f1-score   support

          良性       0.96      0.97      0.97       110
          恶性       0.95      0.93      0.94        61

     micro avg       0.96      0.96      0.96       171
     macro avg       0.96      0.95      0.96       171
  weighted avg       0.96      0.96      0.96       171
    '''
    return None


if __name__ == "__main__":
    logistic()

非监督学习：K-均值聚类（k-means）算法

K-均值聚类属于无监督学习。那么监督学习和无监督学习的区别在哪儿呢？监督学习知道从对象（数据）中学习什么，而无监督学习无需知道所要搜寻的目标，它是根据算法得到数据的共同特征。比如用分类和聚类来说，分类事先就知道所要得到的类别，而聚类则不一样，只是以相似度为基础，将对象分得不同的簇。

K-Means算法有大量的变体，包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。

算法流程

K-means是一个反复迭代的过程，算法分为四个步骤：

1. 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；
   • 我们会根据对数据的先验经验选择一个合适的k值，如果没有什么先验知识，则可以通过交叉验证选择一个合适的k值。
2. 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；
3. 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；
4. 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）

这里发现了一个python2.7版本的简易实现：

from numpy import *
from math import sqrt

def loadDataSet(fileName):      #general function to parse tab -delimited floats
    dataMat = []                #assume last column is target value
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = map(float,curLine) #map all elements to float()
        dataMat.append(fltLine)
    return dataMat
\#计算欧氏距离
def distEclud(vecA, vecB):
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

def randCent(dataSet, k):
    n = shape(dataSet)[1]
    centroids = mat(zeros((k,n)))#create centroid mat
    for j in range(n):#create random cluster centers, within bounds of each dimension
        minJ = min(dataSet[:,j]) 
        rangeJ = float(max(dataSet[:,j]) - minJ)
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))
    return centroids

\#dataSet样本点,k 簇的个数
\#disMeas距离量度，默认为欧几里得距离
\#createCent,初始点的选取
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
    m = shape(dataSet)[0] #样本数
    clusterAssment = mat(zeros((m,2))) #m*2的矩阵                   
    centroids = createCent(dataSet, k) #初始化k个中心
    clusterChanged = True             
    while clusterChanged:      #当聚类不再变化
        clusterChanged = False
        for i in range(m):
            minDist = inf; minIndex = -1
            for j in range(k): #找到最近的质心
                distJI = distMeas(centroids[j,:],dataSet[i,:])
                if distJI < minDist:
                    minDist = distJI; minIndex = j
            if clusterAssment[i,0] != minIndex: clusterChanged = True
            # 第1列为所属质心，第2列为距离
            clusterAssment[i,:] = minIndex,minDist**2
        print centroids

        # 更改质心位置
        for cent in range(k):
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            centroids[cent,:] = mean(ptsInClust, axis=0) 
    return centroids, clusterAssment

伪代码如下：
function K-Means(输入数据，中心点个数K)
获取输入数据的维度Dim和个数N
随机生成K个Dim维的点
while(算法未收敛)
对N个点：计算每个点属于哪一类。
对于K个中心点：
1，找出所有属于自己这一类的所有数据点
2，把自己的坐标修改为这些数据点的中心点坐标
end
输出结果：
end

sklearn.cluster.KMeans(n_clusters=8,init=’k-means++’)

• n_clusters:开始的聚类中心数量
• init:初始化方法，默认为’k-means++’
• labels_:默认标记的类型，可以和真实值比较（不是值比较）